Cho dãy số \(\left( {{u_n}} \right)\) thỏa mãn \({\ln ^2}{u_6} – \ln {u_6} = \ln {u_4} – 1\) và \({u_{n + 1}} = {u_n}.e\) với mọi \(n \ge 1.\) Tìm \({u_1}\)
4. \({e^{ - 3}}\)
Cho hàm số \(y = \frac{{x – 2}}{{x – 1}}\) Đường tiệm cận đứng của đồ thị hàm số là:
4. \(y = 1\)
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f’\left( x \right) = {x^2}\left( {x – 9} \right){\left( {x – 4} \right)^2}.\) Xét hàm số \(y = g\left( x \right) = f\left( {{x^2}} \right)\) trên \(R.\) Trong các phát biểu sau:
I. Hàm số \(y = g\left( x \right)\) đồng biến trên khoảng \(\left( {3; + \infty } \right)\)
II. Hàm số \(y = g\left( x \right)\) nghịch biến trên khoảng \(\left( { – \infty ; – 3} \right)\)
III. Hàm số \(y = g\left( x \right)\)có 5 điểm cực trị
IV. \(\mathop {Min}\limits_{x \in R} g\left( x \right) = f\left( 9 \right)\)
Số phát biểu đúng là
3. 2
Trong không gian tọa độ Oxyz, cho điểm \(A\left( {5;4;3} \right).\) Gọi \(\left( \alpha \right)\) là mặt phẳng đi qua các hình chiếu của A lên các trục tọa độ. Phương trình của mặt phẳng \(\left( \alpha \right)\) là:
3. \(\frac{x}{5} + \frac{y}{4} + \frac{z}{3} = 1\)
Biết \({z_1}\) và \({z_2}\) là hai nghiệm của phương trình \(2{z^2} + \sqrt 3 z + 3 = 0.\) Khi đó giá trị của \(z_1^2 + z_2^2\) là
2. \(\frac{9}{4}\) .
Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên \(R\) thỏa mãn đồng thời các điều kiện sau: \(f\left( x \right) > 0\forall x \in R,f’\left( x \right) = – {e^x}.{f^2}\left( x \right)\forall x \in R\) và \(f\left( 0 \right) = \frac{1}{2}.\) Phương trình tiếp tuyến của đồ thị tại điểm có hoành độ \({x_0} = \ln 2\) là:
1. \(2x - 9y - 2\ln 2 - 3 = 0\)
Bà A gửi tiết kiệm 50 triệu đồng theo kỳ hạn 3 tháng. Sau 2 năm, bà ấy nhận được số tiền cả gốc cả lãi là 73 triệu đồng. Hỏi lãi suất ngân hàng là bao nhiêu một tháng (làm tròn đến hàng phần nghìn)? Biết rằng trong các tháng của kỳ hạn, chỉ cộng thêm lãi chứ không cộng vốn và lãi tháng trước để tính lãi tháng sau, hết một kỳ hạn lãi suất cộng vào vốn để tính lãi trong đủ một kỳ hạn tiếp theo
4. 0,024
Cho hàm số \(y = f\left( x \right)\) xác định, liên tục trên \(R\) và có bảng biến thiên sau: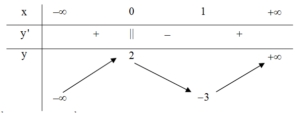
Trong các khẳng định sau, khẳng định nào đúng?
4. Hàm số có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng \( - 3\)
Cho hàm số \(y = a{x^3} + b{{\rm{x}}^2} + c{\rm{x}} + d\) đạt cực trị tại các điểm \({x_1},{x_2}\) thỏa mãn \({x_1} \in \left( { – 1;0} \right);{x_2} \in \left( {1;2} \right).\) Biết hàm số đồng biến trên khoảng \(\left( {{x_1};{x_2}} \right).\) Đồ thị hàm số cắt trục tung tại điểm có tung độ âm. Trong các khẳng định sau, khẳng định nào đúng?
1. \(a < 0,b < 0,c > 0,d < 0\)
\(\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {x + 1} – \sqrt {x – 3} } \right)\) bằng
1. \( - \infty \)
Cho lăng trụ ABC.A’B’C’ có thể tích bằng \(6{{\rm{a}}^3}.\) Các điểm M, N, P lần lượt thuộc các cạnh AA’, BB’, CC’ sao cho \(\frac{{AM}}{{AA’}} = \frac{1}{2},\frac{{BN}}{{BB’}} = \frac{2}{3}.\) Tính thể tích V’ của khối đa diện ABC.MNP
3. \(V' = \frac{9}{{16}}{a^3}\)
Trong không gian tọa độ Oxyz, cho điểm \(A\left( {0;0; – 2} \right)\) và đường thẳng \(\Delta :\frac{{x + 2}}{2} = \frac{{y – 2}}{3} = \frac{{z + 3}}{2}.\) Phương trình mặt cầu tâm A, cắt \(\Delta \) tại hai điểm B và C sao cho \(BC = 8\) là:
2. \({x^2} + {y^2} + {\left( {z + 2} \right)^2} = 25\)
Điểm nào sau đây thuộc cả hai mặt phẳng \(\left( {Oxy} \right)\) và mặt phẳng \(\left( P \right):x + y + z – 3 = 0\)
4. \(M\left( {1;1;0} \right)\)
Cho hình chóp S.ABCD có đáy ABCD là nửa lục giác đều nội tiếp đường tròn đường kính \(AB = 2a,SA = a\sqrt 3 \) và vuông góc với mặt phẳng ABCD. Cosin của góc giữa hai mặt phẳng \(\left( {SAD} \right)\) và \(\left( {SBC} \right)\) bằng
3. \(\frac{{\sqrt 2 }}{5}\)
Cho hình phẳng (S) giới hạn bởi đường cong có phương trình \(y = \sqrt {2 – {x^2}} \) và trục Ox, quay (S) xung quanh Ox. Thể tích của khối tròn xoay được tạo thành bằng
1. \(V = \frac{{4\sqrt 2 \pi }}{3}\)
Cho hai số phức \({z_1},{z_2}\) có điểm biểu diễn lần lượt là \({M_1},{M_2}\) cùng thuộc đường tròn có phương trình \({x^2} + {y^2} = 1\) và \(\left| {{z_1} – {z_2}} \right| = 1.\) Tính giá trị biểu thức \(P = \left| {{z_1} + {z_2}} \right|\)
4. \(P = \sqrt 2 \)
Cho \(\int\limits_0^1 {\frac{{d{\rm{x}}}}{{\sqrt {x + 2} + \sqrt {x + 1} }}} = a\sqrt b – \frac{8}{3}\sqrt a + \frac{2}{3}\left( {a,b \in {N^*}} \right).\) Tính \(a + 2b\)
2. \(a + 2b = 8\)
Cho hàm số \(y = {x^3} – 2x + 1\) có đồ thị \(\left( C \right).\) Hệ số góc của tiếp tuyến với \(\left( C \right)\) tại \(M\left( { – 1;2} \right)\) bằng
4. 25
Giá trị lớn nhất của hàm số \(f\left( x \right) = {x^3} – 8{{\rm{x}}^2} + 16{\rm{x}} – 9\) trên đoạn \(\left[ {1;3} \right]\) là
2. \(\mathop {\max }\limits_{\left[ {1;3} \right]} f\left( x \right) = - 6\)
Phần ảo của số phức \(z = 5 + 2i\) bằng
3. 2i
Hệ số của số hạng chứa \({x^3}\) trong khai triển \({\left( {\frac{1}{x} + {x^3}} \right)^9}\) (với \(x \ne 0)\) bằng
4. \(54{x^3}\)
Số giao điểm tối đa của 10 đường thẳng phân biệt là
4. 50
Tập xác định của hàm số \(y = {\left( {x – 1} \right)^{\frac{1}{2}}}\) là
3. \(\left( {1; + \infty } \right)\)
Cho x, y là các số thực dương thay đổi. Xét hình chóp S.ABC có \(SA = x,BC = y,\) các cạnh còn lại đều bằng 1. Khi thể tích khối chóp S,ABC đạt giá trị lớn nhất thì tích x.y bằng
1. \(\frac{4}{3}\)
Trong không gian Oxyz, cho tam giác ABC, biết \(A\left( {1; – 2;4} \right),B\left( {0;2;5} \right),C\left( {5;6;3} \right).\) Tọa độ trọng tâm G của tam giác ABC là
1. \(G\left( {2;2;4} \right)\)
Công thức tính thể tích V của khối cầu có bán kính bằng R là
3. \(V = \frac{4}{3}\pi {R^2}\)
Cho hình trụ có bán kính đáy bằng a, diện tích toàn phần bằng \(8\pi {a^2}.\) Chiều cao của hình trụ bằng
2. 2a
Phương trình \({\log _3}\left( {x + 2} \right) + \frac{1}{2}{\log _3}{\left( {x – 5} \right)^2} + {\log _{\frac{1}{3}}}8 = 0\) có tất cả bao nhiêu nghiệm thực?
3. 4
Nguyên hàm \(F\left( x \right)\) của hàm số \(f\left( x \right) = 3 – \frac{1}{{{{\sin }^2}x}}\) là
3. \(F\left( x \right) = 3{\rm{x}} + \tan x + C\)
Cho số phức z thỏa mãn \(\left| {\frac{{z – 1}}{{z + 3i}}} \right| = \frac{1}{{\sqrt 2 }}.\) Tìm giá trị lớn nhất của biểu thức \(P = \left| {z + i} \right| + 2\left| {\overline z – 4 + 7i} \right|\)
2. 20
Trong không gian tọa độ Oxyz, cho \(M\left( {2;0;0} \right),N\left( {1;1;1} \right).\) Mặt phẳng (P) thay đổi qua M, N và cắt các trục Oy, Oz lần lượt tại \(B\left( {0;b;0} \right),C\left( {0;0;c} \right)\left( {b > 0,c > 0} \right).\) Hệ thức nào dứoi đây là đúng?
1. \(b + c = bc\)
Cho hàm số \(f\left( x \right)\) xác định trên \(R\backslash \left\{ { – 2;1} \right\}\) thỏa mãn \(f’\left( x \right) = \frac{1}{{{x^2} + x – 2}},f\left( { – 3} \right) – f\left( 3 \right) = 0\) và \(f\left( 0 \right) = \frac{1}{3}.\) Giá trị biểu thức \(f\left( { – 4} \right) + f\left( { – 1} \right) – f\left( 4 \right)\) bằng
1. \(\frac{1}{3}\ln 2 + \frac{1}{3}\)
Cho hàm số \(y = \frac{{x + 3}}{{x + 2}}.\) Khẳng định nào sau đây đúng?
4. Hàm số nghịch biến trên các khoảng \(\left( { - \infty ; - 2} \right)\) và \(\left( { - 2; + \infty } \right)\)
Đồ thị dưới đây là của hàm số nào?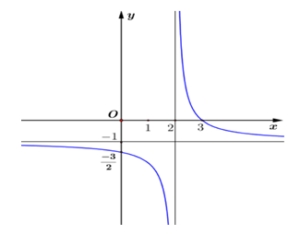
1. \(y = \frac{{ - x - 3}}{{x - 2}}\)
Cho A, B là hai biến cố xung khắc. Biết \(P\left( A \right) = \frac{1}{3},P\left( B \right) = \frac{1}{4}.\) Tính \(P\left( {A \cup B} \right)\)
1. \(\frac{1}{7}\)
Trong không gian tọa độ Oxy, cho tam giác ABC biết \(A\left( {1;0; – 1} \right),\,\,B\left( {2;3; – 1} \right),\,\,C\left( { – 2;1;1} \right)\). Phương trình đường thẳng đi qua tâm đường tròn ngoại tiếp cảu tam giác ABC và vuông góc với mặt phẳng \(\left( {ABC} \right)\).
1. \(\frac{x}{3} = \frac{{y - 2}}{1} = \frac{z}{5}\)
Số gí trị nguyên dương của tham số m để hàm số \(y = {\left( {\frac{1}{2}} \right)^{{x^3} – 6{{\rm{x}}^2} + m{\rm{x}} + 2}}\) luôn đồng biến trên khoảng \(\left( {1;3} \right)\) là:
2. 10
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f’\left( x \right)\) liên tục trên đoạn \(\left[ {1;4} \right],f\left( 1 \right) = 12\) và \(\int\limits_1^4 {f’\left( x \right)d{\rm{x}} = 17.} \) Giá trị của \(f\left( 4 \right)\) bằng
1. 29.
Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên đoạn \(\left[ {a;b} \right].\) Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right),\) trục hoành và hai đường thẳng \(x = a,x = b\) được tính theo công thức:
1. \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|} d{\rm{x}}\)
Diện tích xung quanh của hình nón được sinh ra khi quay tam giác đều ABC cạnh a xung quanh đường cao AH
2. \(\frac{{\pi {a^2}}}{2}\)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SAC} \right)\) cùng vuông góc với đáy \(\left( {ABCD} \right)\) và \(SA = 2a.\) Tính cosin của góc giữa đường thẳng SB và mặt phẳng \(\left( {SAD} \right)\)
2. \(\frac{1}{2}\)
Cho mặt phẳng \(\left( \alpha \right)\) có phương trình: \(2{\rm{x}} + 4y – 3{\rm{z}} + 1 = 0,\) một vecto pháp tuyến của mặt phẳng \(\left( \alpha \right)\) là
2. \(\overrightarrow n = \left( { - 3;4;2} \right)\)
Trong không gian tọa độ Oxyz cho các điểm \(A\left( {1;2;3} \right),B\left( {2;1;0} \right),C\left( {4; – 3; – 2} \right),D\left( {3; – 2;1} \right),E\left( {1;1; – 1} \right).\) Hỏi có bao nhiêu mặt phẳng cách đều 5 điểm trên?
3. không tồn tại
Tập nghiệm của bất phương trình \({\log _2}\left( {x + 1} \right) < {\log _2}\left( {3 - x} \right)\) là
4. \(S = \left( {1; + \infty } \right)\)
Cho hàm số \(y = f\left( x \right) > 0\) xác định, có đạo hàm trên đoạn \(\left[ {0;1} \right]\) và thỏa mãn:
\(g\left( x \right) = 1 + 2018\int\limits_0^x {f\left( t \right)} dt,g\left( x \right) = {f^2}\left( x \right).\) Tính \(\int\limits_0^1 {\sqrt {g\left( x \right)} d{\rm{x}}} \)
1. 505
Cho hình chóp S.ABCD có \(SA \bot \left( {ABC{\rm{D}}} \right)\), đáy ABCD là hình vuông cạnh bằng 4, biết \(SA = 3.\) Khoảng cách giữa 2 đường thẳng SB và AD là
2. \(\frac{{12}}{5}\)
Tổng tất các nghiệm thuộc đoạn \(\left[ {0;10\pi } \right]\) của phương trình \({\sin ^2}2{\rm{x}} + 3\sin 2{\rm{x}} + 2 = 0\).
1. \(\frac{{299}}{4}\pi \)
Có 12 người xếp thành một hàng dọc (vị trí của mỗi người trong hàng là cố định). Chọn ngẫu nhiên 3 người trong hàng. Tính xác suất để 3 người được chọn không có 2 người nào đứng cạnh nhau
2. \(\frac{7}{{110}}\)
Cho phương trình \({2.5^x} – \left( {m + 2} \right){5^x} + 2m – 1 = 0\) với m là tham số thực. Có bao nhiêu giá trị nguyên \(m \in \left[ {0;2018} \right]\) để phương trình có nghiệm?
2. 2018
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ bên. Phương trình \(f\left( x \right) = – 3\) có số nghiệm là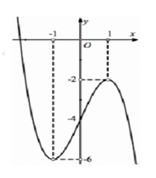
4. 0
Kết quả:
Tải PDF tài liệu học tập đang trở thành lựa chọn phổ biến cho sinh viên và người đi làm nhờ tính tiện lợi và tiết kiệm thời gian. Tài liệu PDF cung cấp nhiều nội dung từ sách PDF, tài liệu nghiên cứu, đến giáo trình chuyên ngành, giúp người dùng dễ dàng lưu trữ và truy cập trên các thiết bị số. Việc sử dụng tài liệu PDF không chỉ giúp tăng cường kiến thức mà còn hỗ trợ học tập và làm việc hiệu quả hơn.