Tập xác định của hàm số \(y = {x^2} – 2024x + 2025\) là
4. \(\left( { - \infty ;\, + \infty } \right)\).
Tập xác định của hàm số \(y = \frac{{x – 3}}{{4x – 4}}\) là
1. \(\mathbb{R}\backslash \left\{ 1 \right\}\).
Tập xác định của hàm số \(y = \frac{{2025}}{{{x^2} – 9}}\) là
2. \(\mathbb{R}\backslash \left\{ { - 3;3} \right\}\).
Tập xác định \(D\) của hàm số \(y = \sqrt {3x – 1} \) là
3. \(D = \left[ {\frac{1}{3}; + \infty } \right)\).
Tập xác định của hàm số \(y = \sqrt {4 – x} + \sqrt {x – 2} \) là
2. \(D = \left[ {2;4} \right]\)
Tập xác định của hàm số \(y = \sqrt {9 – x} + \frac{x}{{\sqrt {x – 1} }}\) là \(\left( {a;b} \right]\) với \(a,b\) là các số thực. Tính tổng \(a + b\).
4. \(a + b = 10\).
Với giá trị nào của \(m\) thì hàm số \(y = \frac{{2x + 1}}{{{x^2} – 2x – 3 – m}}\) xác định trên \(\mathbb{R}\).
2. \(m < - 4\).
Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau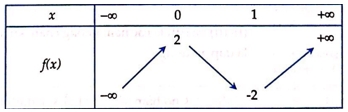
Hàm số nghịch biến trong khoảng nào dưới đây?
4. \(\left( {0;1} \right)\)
Cho hàm số có đồ thị như hình bên dưới.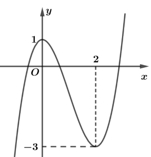
Khẳng định nào sau đây là đúng?
3. Hàm số nghịch biến trên khoảng \(\left( {0;2} \right)\).
Cho \((P)\) có phương trình \(y = {x^2} – 2x + 4\). Điểm nào sau đây thuộc đồ thị \((P)\).
4. \(M\left( { - 3;19} \right)\).
Kết quả:
Tải PDF tài liệu học tập đang trở thành lựa chọn phổ biến cho sinh viên và người đi làm nhờ tính tiện lợi và tiết kiệm thời gian. Tài liệu PDF cung cấp nhiều nội dung từ sách PDF, tài liệu nghiên cứu, đến giáo trình chuyên ngành, giúp người dùng dễ dàng lưu trữ và truy cập trên các thiết bị số. Việc sử dụng tài liệu PDF không chỉ giúp tăng cường kiến thức mà còn hỗ trợ học tập và làm việc hiệu quả hơn.