Cho hàm số \(y = a{x^4} + b{x^2} + c{\text{ }}\left( {a,b,c \in \mathbb{R}} \right)\) có đồ thị như hình vẽ bên. Số điểm cực tiểu của hàm số đã cho là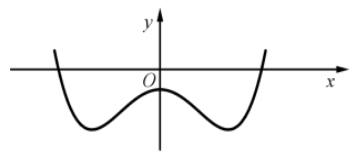
3. 2
Đồ thị hàm số nào dưới đây có dạng đường cong như hình bên? 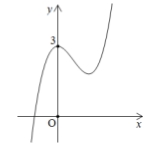
4. \(y = {x^3} - 2{x^2} + 3\)
Cho hàm số y=f(x) có bảng biến thiên như sau. Số nghiệm thực của phương trình 2f(x) + 3 = 0 ?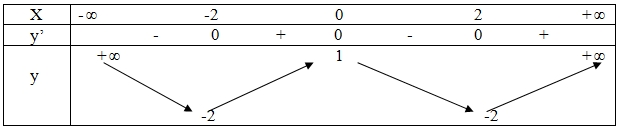
1. 1.
Đường tiệm cận ngang của đồ thị hàm số \(y = \frac{{ – 2x + 3}}{{ – x + 1}}\) là đường thẳng
3. \(x = 1\)
Cho hàm số \(y = f(x)\) có bảng xét dấu đạo hàm như sau, Mệnh đề nào dưới đây đúng ?
1. Hàm số đồng biến trên khoảng \(( - 2;0)\).
Cho hàm số \(y = f(x)\)có bảng biến thiên dưới đây. Hàm số \(y = f(x)\) đồng biến trên khoảng nào ?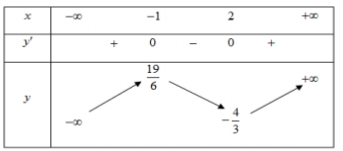
4. \(( - \infty ; - 1)\)
Tính thể tích V của khối chóp có đáy là hình vuông cạnh bằng 5 và chiều cao bằng 6.
3. \(V = 150\)
Tìm GTNN m của hàm số \(y = {x^3} – 7{x^2} + 11x – 2\) trên đoạn [0;3].
2. m=-2.
Khối đa điện nào sau đây có công thức tính thể tích là \(V = B.h\) (B là diện tích đáy ; h là chiều cao)
1. Khối lập phương.
Số cạnh của một hình bát diện đều là:
4. Sáu
Cho hàm số \(y = f(x)\)xác điịnh, liên tục trên R và có bảng xét dấu \(f'(x)\) như sau, hàm số \(y = f(x)\) có bao nhiêu cực đại?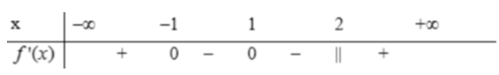
1. 3
Cho hàm số y = f(x) có bảng biến thiên như sau: 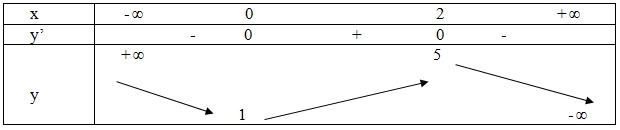 Giá trị cực tiểu của hàm số đã cho bằng
Giá trị cực tiểu của hàm số đã cho bằng
1. 0
Cho hàm số \(y = {x^4} – 2{x^2}\). Mệnh đề nào dưới đây đúng ?
2. Hàm số đồng biến trên khoảng \(( - \infty ; - 2)\).
Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(y = – {x^3} + 3{x^2} – 1\) trên đoạn \(\left[ { – 1;1} \right]\). Giá trị của M +3m bằng:
1. 0
cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, \(SA \bot (ABCD)\), SC tạo với mặt đáy một góc bằng \({30^0}\). Tính thể tích V của khối chóp đã cho
1. . \(\frac{{{a^3}\sqrt 6 }}{9}\)
Tìm số tiệm cận đứng và ngang của đồ thị hàm số \(y = \frac{{\sqrt {x + 4} + 2}}{{{x^2} + x}}\).
4. 3.
Nếu phương trình \({x^3} – 3{x^2} – m = 0\) có 1 nghiệm thì
1. \(m < - 4 \vee m > 0\)
Cho hình chóp S.ABC có thể tích \(V\). Gọi M là một điểm trên cạnh BC sao cho \(CM = 2BM\)và \({V_1},\,{V_2}\) lần lượt là thể tích của các khối chóp \(S.ABM,\,\,S.AMC\). Tìm kết luận sai?
2. \(V = 3.{V_2}\)
Cho khối chóp S.ABC có \(SA \bot (ABC)\), tam giác ABC vuông ở C, \(AC = a\sqrt 2 \), \(BC = a\). Tính thể tích khối chóp S.ABC biết rằng \(SB = 2a\).
2. \(\frac{{{a^3}\sqrt 6 }}{6}\)
Tìm tất cả các giá trị của m để hàm số \(f(x) = \frac{{mx + 1}}{{x – m}}\)có GTNN trên \(\left[ {1;2} \right]\) bằng 2.
3. m = 2
Thể tích khối lăng trụ tam giác đều có cạnh đáy bằng a và cạnh bên bằng 3a là:
2. \(\frac{{3{a^3}\sqrt 3 }}{4}\)
một chất điểm chuyển động có phương trình chuyển động là \(s = – {t^3} + 6{t^2} + 3t\), với t ( giây) là khoảng thời gian kể từ lúc vật bắt đầu chuyển động và s( mét) là quảng đường vật đi được trong khoảng thời gian đó. Trong khoảng thời gian 6 giây đầu tiên, vận tốc \(v(m/s)\) của chất điểm đạt giá trị lớn nhất bằng:
4. \(27m/s\)
Đồ thị của hàm số \(y = {x^4} – 2{x^2} + 2\) và đồ thị của hàm số \(y = – 3{x^2} – 2\) có tất cả bao nhiêu điểm chung.
4. 1.
Có tất cả bao nhiêu giá trị nguyên dương của m để hàm số \(y = m{x^4} + (m – 2023){x^2} + 2024\) có 3 điểm cực trị?
1. 2022
Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại B với \(BA = 2a,AC = a\sqrt 5 \). Biết A'B hợp với đáy một góc \({60^0}\). Tính thể tích V của khối lăng trụ ABC.A'B'C'.
1. \(2{a^3}\sqrt 3 \)
có bao nhiêu giá trị nguyên của tham số \(m \leqslant 5\) sao cho hàm số \(y = {x^3} + 3{x^2} + mx + m\)đồng biến trên R?
1. 3
Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Cạnh bên SA vuông góc với mặt phẳng đáy và SA = 2AB. Gọi M là trung điểm của cạnh SC, mp(Q) chứa AM và song song với BD cắt SB tại N và cắt SD tại P. Gọi \({V_1}\) và \({V_2}\) lần lượt là thể tích của khối chóp S.ANMP và khối đa diện ABCDPMN. Tỉ số \(\frac{{{V_1}}}{{{V_2}}}\) bằng:
2. \(\frac{1}{2}\)
Cho hình chóp S.ABC có thể tích \(V\). Gọi M, N, P lần lượt là trung điểm của các cạnh SA, SB, SC và \({V_1},\,{V_2}\) lần lượt là thể tích của khối chóp S.MNP và khối chóp cụt MNP.ABC. Tìm kết luận đúng?
4. \(V = {V_1} + {V_2}\)
Cho lăng trụ tam giác đều ABC.A'B'C' có thể tích \({V_{}}.\) Trên AB lấy điểm \(M\) sao cho\(AM = 2MB\) . N, P lần lượt là trung điểm của B'B và A'C' . Mặt phẳng \(\left( {MNP} \right)\) chia khối lăng trụ ABC.A'B'C' thành hai khối đa diện, trong đó khối đa diện chứa đỉnh A' có thể tích \({V_1},\) Tỉ số \(\frac{{{V_1}}}{{{V_2}}}\) bằng
2. \(\frac{{95}}{{144}}.\)
Cho hàm số \(f'(x)\) có đồ thị như hình vẽ bên. Hàm số \(g(x) = f(3x + 1) + 9{x^3} + \frac{9}{2}{x^2}\) đồng biến trên khoảng nào dưới đây? 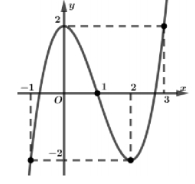
4. \(( - 2;0)\)
Cho hàm số \(y = f(x)\) có đạo hàm liên tục trên R, bảng biến thiên của hàm số \(f'(x)\) như sau, số điểm cực trị của hàm số \(y = f({x^2} + 2x)\) là: 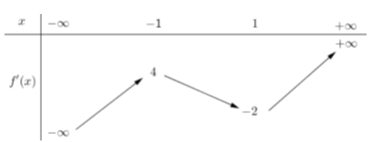
2. 4
Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị như hình vẽ bên. Số nghiệm thực của phương trình \(\left| {f\left( {{x^3} – 3x} \right)} \right| = \frac{1}{2}\) là 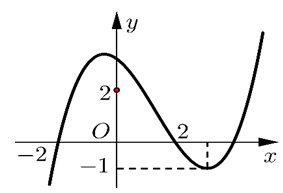
1. 10
Kết quả:
Tải PDF tài liệu học tập đang trở thành lựa chọn phổ biến cho sinh viên và người đi làm nhờ tính tiện lợi và tiết kiệm thời gian. Tài liệu PDF cung cấp nhiều nội dung từ sách PDF, tài liệu nghiên cứu, đến giáo trình chuyên ngành, giúp người dùng dễ dàng lưu trữ và truy cập trên các thiết bị số. Việc sử dụng tài liệu PDF không chỉ giúp tăng cường kiến thức mà còn hỗ trợ học tập và làm việc hiệu quả hơn.