Tìm tất cả các giá trị dương của tham số \(m\) để hàm số \(f\left( x \right) = m{x^2} – 4x – {m^2}\) luôn nghịch biến trên \(\left( { – 1;2} \right)\).
3. \(0 < m \leqslant 1\).
Tìm giá trị của tham số \(m\) để đỉnh \(I\) của đồ thị hàm số \(y = – {x^2} + 6x + m\) thuộc đường thẳng \(y = x + 2024\).
4. \(m = 2018\).
Cho parabol \((p):y = a{x^2} + bx + c\) có trục đối xứng là đường thẳng \(x = 1\). Khi đó \(4a + 2b\) bằng
2. \(0\).
Parabol \(y = a{x^2} + bx + c\) đi qua \(A\left( {8;0} \right)\) và có đỉnh \(I\left( {6; – 12} \right)\). Khi đó tích \(a.b.c\) bằng
1. \( - 10368\).
Cho parabol \(y = a{x^2} + bx + c\) có đồ thị như hình sau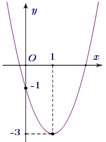
Phương trình của parabol này là
4. \(y = 2{x^2} - 4x - 1\).
Cho parabol \((P):y = a{x^2} + bx + c\), \(\left( {a \ne 0} \right)\) có đồ thị như hình bên dưới.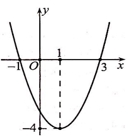
Khi đó \(2a + b + 2c\) có giá trị là:
3. \( - 6\).
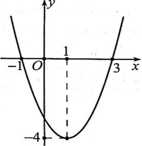Parabol \((P):y = a{x^2} + bx + c,\;(a \ne 0)\) đi qua các điểm \(A( – 1;0),\;B(1; – 4),\;C(3;0)\)Cho hàm số \(y = a{x^2} + bx + c\) có đồ thị như bên.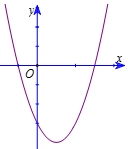
Khẳng định nào sau đây đúng?
1. \(a > 0,b < 0,c < 0.\).
Đồ thị trong hình vẽ dưới đây là của hàm số nào trong các phương án A;B;C;D sau đây?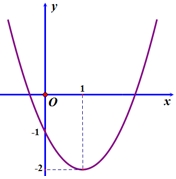
4. \(y = {x^2} - 2x - 1\).
Cho parabol \(y = a{x^2} + bx + c\) có đồ thị như hình sau: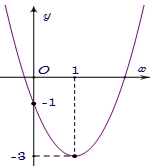
Phương trình của parabol này là
4. \(y = 2{x^2} - 4x - 1.\)
Giá trị lớn nhất của hàm số \(y = – 3{x^2} + 2x + 1\) trên đoạn \(\left[ {1;3} \right]\) là:
2. 0
Kết quả:
Tải PDF tài liệu học tập đang trở thành lựa chọn phổ biến cho sinh viên và người đi làm nhờ tính tiện lợi và tiết kiệm thời gian. Tài liệu PDF cung cấp nhiều nội dung từ sách PDF, tài liệu nghiên cứu, đến giáo trình chuyên ngành, giúp người dùng dễ dàng lưu trữ và truy cập trên các thiết bị số. Việc sử dụng tài liệu PDF không chỉ giúp tăng cường kiến thức mà còn hỗ trợ học tập và làm việc hiệu quả hơn.