Số phức có phần thực bằng \(3\) và phần ảo bằng \(4\) là
1. \(3 + 4i\)
Trong không gian \(Oxyz\), cho mặt cầu \(\left( S \right):{\left( {x + 1} \right)^2} + {\left( {y – 3} \right)^2} + {z^2} = 9\). Tâm của \(\left( S \right)\) có tọa độ là
2. \(\left( { - 1;3;0} \right)\).
Tọa độ tâm đối xứng của đồ thị hàm số \(y = {x^3} – 3x + 2\).
1. \(\left( {0;2} \right)\).
Tình diện tích mặt cầu \(\left( S \right)\) khi biết nửa chu vi đường tròn lớn của nó bằng \(4\pi \).
4. \(S = 16\pi \).
Nguyên hàm của hàm số \(f\left( x \right) = {x^3} + x\) là
1. \(\frac{1}{4}{x^4} + \frac{1}{2}{x^2} + C\)
Cho hàm số \(y = f(x)\) liên tục trên \(\mathbb{R}\) và có bảng xét dấu \(f'(x)\) như sau: Hàm số \(y = f(x)\) có bao nhiêu điểm cực trị?
Hàm số \(y = f(x)\) có bao nhiêu điểm cực trị?
4. 4.
Tìm tập nghiệm \(S\)của bất phương trình \({\log _{\frac{1}{2}}}\left( {x + 1} \right) < {\log _{\frac{1}{2}}}\left( {2x - 1} \right)\).
4. \(S = \left( {\frac{1}{2};2} \right)\).
Cho khối lăng trụ có diện tích đáy bằng \({a^2}\sqrt 3 \), khoảng cách giữa hai đáy của lăng trụ bằng \(a\sqrt 6 \). Tính thể tích \(V\) của khối lăng trụ
1. \(V = 3{a^3}\sqrt 2 \)
Tập xác định của hàm số \(y = {\left( {4 – 3x – {x^2}} \right)^{ – 2022}}\) là
1. \(\mathbb{R}\backslash \left\{ { - 4;1} \right\}.\)
Tìm nghiệm của phương trình \({3^{x – 1}} = 27\)
4. \(x = 4\)
Nếu \(\int\limits_0^2 {f\left( x \right){\text{d}}x} = 2\) thì \(\int\limits_0^2 {\left[ {4x – f\left( x \right)} \right]{\text{d}}x} \) bằng
4. \(6\).
Cho hai số phức \({z_1} = – 3 + i\) và \({z_2} = 1 – i.\) Phần ảo của số phức \({z_1} + \overline {{z_2}} \)bằng
3. \(2.\)
Trong không gian \(Oxyz\), một vectơ pháp tuyến của mặt phẳng \(\frac{x}{{ – 2}} + \frac{y}{{ – 1}} + \frac{z}{3} = 1\) là.
4. \(\overrightarrow n = \left( {3;\,6;\, - 2} \right)\)
Trong không gian \(Oxyz,\) cho điểm \(M\left( {1;\, – 2;\,3} \right)\). Toạ độ điểm \(A\) là hình chiếu vuông góc của \(M\) trên mặt phẳng \(\left( {Oyz} \right)\) là
4. \(\left( {0;\, - 2;\,3} \right)\).
Trong mặt phẳng tọa độ \(Oxy\), 3 điểm \(A,B,C\) lần lượt là điểm biểu diễn của ba số phức\({z_1} = 3 – 7i,{z_2} = 9 – 5i\)và \({z_3} = – 5 + 9i\). Khi đó, trọng tâm \(G\) là điểm biểu diễn của số phức nàosau đây?
3. \(z = \frac{7}{3} - i\).
Phương trình đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số \(y = \frac{{x + 1}}{{2 – x}}\) lần lượt là
1. \(x = 2;y = - 1\).
Với \(a > 0\)đặt \({\log _2}\left( {2a} \right) = b\), khi đó \({\log _2}\left( {8{a^4}} \right)\) bằng
4. \(4b - 1\).
Trong các hàm số sau, hàm số nào có đồ thị như hình vẽ dưới?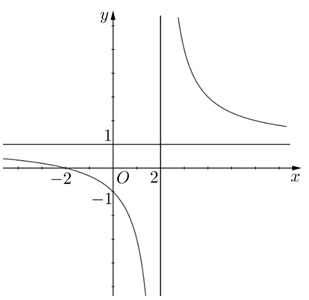
1. \(y = \frac{{x + 2}}{{x - 2}}\).
Trong không gian \(Oxyz\) cho đường thẳng \(d{\text{ }}:{\mkern 1mu} \frac{{x – 2}}{3} = \frac{{y + 1}}{{ – 1}} = \frac{{z + 3}}{2}\). Điểm nào sau đây không thuộc đường thẳng \(d\)?
2. \(M\left( { - 2;1;3} \right)\)
Số cách chọn 2 học sinh từ 8 học sinh là
1. \(C_8^2\).
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh \(a\). Biết \(SA \bot \left( {ABC} \right)\) và \(SA = a\sqrt 3 \). Tính thể tích khối chóp \(S.ABC\).
3. \(\frac{{{a^3}}}{4}\)
Tìm đạo hàm của hàm số \(y = {\text{log}}\,x\).
2. \(y' = \frac{1}{{x\ln 10}}\)
Cho hàm số \(y = f\left( x \right)\) có bảng xét dấu của đạo hàm như sau: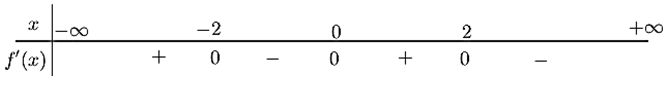 Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
3. \(\left( { - 2;0} \right)\).
Một hình nón có đường kính đáy là \(2a\sqrt 3 \), góc ở đỉnh là \({120^0}\). Tính thể tích của khối nón đó theo \(a\).
2. \(\pi {a^3}\).
Cho hàm số \(f\left( x \right)\) liên tục, có đạo hàm trên \(\left[ { – 1;2} \right],f\left( { – 1} \right) = 8;f\left( 2 \right) = – 1\). Tích phân \(\int\limits_{ – 1}^2 {f'\left( x \right)} dx\) bằng
3. \( - 9.\)
Cho cấp số cộng \(\left( {{u_n}} \right)\) với \({u_1} = 2\) và \({u_2} = 7\). Công sai của cấp số cộng đã cho bằng
1. \(5\).
Cho hàm số \(f\left( x \right) = 2x + {e^x}\). Tìm một nguyên hàm \(F\left( x \right)\) của hàm số \(f\left( x \right)\) thỏa mãn \(F\left( 0 \right) = 2023\).
1. \(F\left( x \right) = {x^2} + {e^x} + 2022\).
Cho hàm đa thức \(y = f\left( x \right)\) có đồ thị như hình vẽ sau: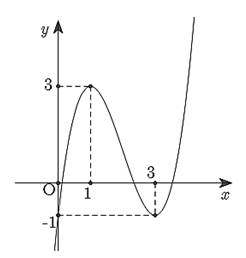 Điểm cực tiểu của hàm số đã cho là
Điểm cực tiểu của hàm số đã cho là
3. \(x = 3\).
Trên đoạn \(\left[ { – 4\,;\, – 1} \right]\), hàm số \(y = {x^4} – 8{x^2} + 13\) đạt giá trị nhỏ nhất tại điểm
1. \(x = - 2\).
Hàm số nào dưới đây đồng biến trên khoảng \(\left( { – \infty ; + \infty } \right)\)?
2. \(y = {x^3} + x\)
Xét tất cả các số dương \(a\) và \(b\) thỏa mãn \({\log _2}a = {\log _8}(ab)\). Mệnh đề nào dưới đây đúng?
4. \({a^2} = b\).
Cho hình chóp \(S.ABCD\) có tất cả các cạnh bằng nhau (tham khảo hình bên).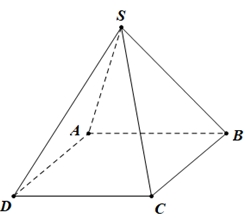 Góc giữa hai đường thẳng \(SC\) và \(AB\) bằng
Góc giữa hai đường thẳng \(SC\) và \(AB\) bằng
2. \({60^0}\).
Biết \(\int\limits_1^2 {f\left( x \right)} {\mkern 1mu} {\text{d}}x = 3\) và \(\int\limits_1^2 {g\left( x \right)} {\text{d}}x = 2\). Khi đó \(\int\limits_1^2 {\left[ {f\left( x \right) – g\left( x \right)} \right]} {\mkern 1mu} {\text{d}}x\) bằng?
2. \(1\).
Trong không gian \(Oxyz\) cho điểm \(A\left( {1; – 1;2} \right)\) và mặt phẳng \(\left( P \right):2x – y + 3z + 1 = 0\). Mặt phẳng đi qua \(A\) và song song với mặt phẳng \(\left( P \right)\) có phương trình là
4. \(2x - y + 3z - 9 = 0\).
Cho số phức \(z\) thỏa mãn \(z + 2i.\overline z = 1 + 17i\). Khi đó \(\left| z \right|\) bằng
1. \(\sqrt {146} \).
Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bên bằng \(2a\) (tham khảo hình vẽ). Khoảng cách từ \(C\) đến mặt phẳng \(\left( {BDD'B'} \right)\) bằng 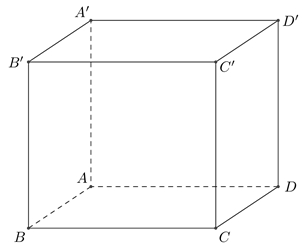
3. \(\sqrt 2 a\).
Chọn ngẫu nhiên đồng thời hai số từ tập hợp gồm 19 số nguyên dương đầu tiên. Xác suất để chọn được hai số chẵn bằng
3. \(\frac{4}{{19}}\).
Trong không gian \(Oxyz\), đường thẳng đi qua điểm \(M\left( { – 2;\,1;\,3} \right)\) và nhận vectơ \(\overrightarrow u = \left( {1; – 3;\,5} \right)\) làm vectơ chỉ phương có phương trình là:
4. \(\frac{{x + 2}}{1} = \frac{{y - 1}}{{ - 3}} = \frac{{z - 3}}{5}\).
Có bao nhiêu số nguyên \(x\) thỏa mãn \(\left[ {{{\log }_2}\left( {{x^2} + 1} \right) – {{\log }_2}\left( {x + 31} \right)} \right]\left( {32 – {2^{x – 1}}} \right) \geqslant 0\)?
1. 27.
Cho hàm số \(f\left( x \right) = a{x^4} + b{x^3} + c{x^2}\left( {a,b,c \in \mathbb{R}} \right)\). Hàm số \(y = f'\left( x \right)\) có đồ thị như trong hình bên. 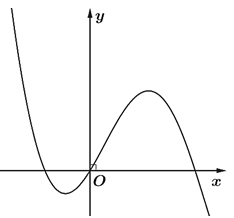 Số nghiệm thực phân biệt của phương trình \(3f\left( x \right) + 4 = 0\) là
Số nghiệm thực phân biệt của phương trình \(3f\left( x \right) + 4 = 0\) là
2. \(2\).
Cho \(f\left( x \right)\) là hàm số liên tục trên tập số thực \(\mathbb{R}\) và thỏa mãn \(f\left( {{x^3} + 3x + 1} \right) = x + 2\). Tính \(I = \int\limits_1^5 {f\left( x \right){\text{d}}x.} \)
1. \(\frac{{41}}{4}\).
Cho hình lập phương \(ABCD.A'B'C'D'\) cạnh bằng \(1\). Gọi \(M\) là trung điểm cạnh \(BB'\). Mặt phẳng \((MA'D)\) cắt cạnh \(BC\) tại \(K\). Thể tích khối đa diện lồi \(A'B'C'D'MKCD\) bằng
4. \(\frac{{17}}{{24}}\).
Có tất cả bao nhiêu số nguyên \(m\) để phương trình \({z^2} + mz + 5 = 0\) có hai nghiệm phức \({z_1},{z_2}\) thoả mãn \(\left| {{z_1}} \right| + \left| {{z_2}} \right| = 2\sqrt 5 \).
1. 9.
Cho các số phức \(z\) thoả mãn \(\left| z \right| = 2\). Đặt \(w = \left( {1 + 2i} \right)z – 1 + 2i\). Tìm giá trị nhỏ nhất của \(\left| w \right|\).
4. \(\sqrt 5 \).
Cho \(f\left( x \right),\,g\left( x \right)\) lần lượt là các hàm đa thức bậc ba và bậc nhất có đồ thị như hình vẽ bên dưới: 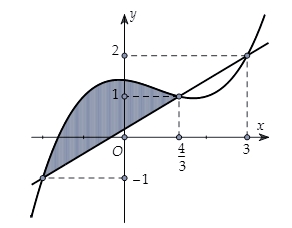 Biết diện tích hình \(S\)(được tô đậm) bằng \(\frac{{250}}{{81}}\). Tính \(\int\limits_0^2 {f\left( x \right){\text{d}}x} \).
Biết diện tích hình \(S\)(được tô đậm) bằng \(\frac{{250}}{{81}}\). Tính \(\int\limits_0^2 {f\left( x \right){\text{d}}x} \).
1. \(\frac{{34}}{{15}}\).
Trong không gian \(Oxyz\), cho đường thẳng \(d\): \(\frac{x}{2} = \frac{{y – 3}}{1} = \frac{{z – 2}}{{ – 3}}\) và mặt phẳng \(\left( P \right)\): \(x – y + 2z – 6 = 0\). Đường thẳng nằm trong mặt phẳng \(\left( P \right)\), cắt và vuông góc với \(d\) có phương trình là
1. \(\frac{{x + 2}}{1} = \frac{{y - 2}}{7} = \frac{{z - 5}}{3}\).
Cho hình trụ có chiều cao bằng \(5\sqrt 3 \). Cắt hình trụ đã cho bởi mặt phẳng song song với trục và cách trục một khoảng bằng 1, thiết diện thu được có diện tích bằng 30. Diện tích xung quanh của hình trụ đã cho bằng
3. \(20\sqrt 3 \pi \).
Có bao nhiêu cặp số nguyên thoả mãn \(0 < y < 2020\) và \({3^x} + 3x - 6 = 9y + {\log _3}{y^3}\)?
2. \(7\).
Trong không gian \(Oxyz\) cho 3 điểm \(A\left( {9\,;\,0\,;\,0} \right)\), \(B\left( {0\,;\,6\,;\,6} \right)\), \(C\left( {0\,;\,0\,;\, – 16} \right)\) và điểm \(M\) di động trên mặt phẳng \(\left( {Oxy} \right)\). Tìm giá trị lớn nhất của \(S = \left| {\left| {\overrightarrow {MA} + 2\overrightarrow {MB} } \right| – 3MC} \right|\).
1. \(39\).
Cho hàm số \(f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\). Đồ thị của hàm số \(y = f\left( {5 – 2x} \right)\) như hình vẽ bên dưới: 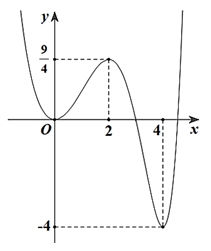 Có bao nhiêu giá trị thực của tham số \(m\)thuộc khoảng \(\left( { – 9;9} \right)\) thỏa mãn \(2m \in \mathbb{Z}\) và hàm số \(y = \left| {2f\left( {4{x^3} + 1} \right) + m – \frac{1}{2}} \right|\) có 5 điểm cực trị ?
Có bao nhiêu giá trị thực của tham số \(m\)thuộc khoảng \(\left( { – 9;9} \right)\) thỏa mãn \(2m \in \mathbb{Z}\) và hàm số \(y = \left| {2f\left( {4{x^3} + 1} \right) + m – \frac{1}{2}} \right|\) có 5 điểm cực trị ?
1. 26.
Kết quả:
Tải PDF tài liệu học tập đang trở thành lựa chọn phổ biến cho sinh viên và người đi làm nhờ tính tiện lợi và tiết kiệm thời gian. Tài liệu PDF cung cấp nhiều nội dung từ sách PDF, tài liệu nghiên cứu, đến giáo trình chuyên ngành, giúp người dùng dễ dàng lưu trữ và truy cập trên các thiết bị số. Việc sử dụng tài liệu PDF không chỉ giúp tăng cường kiến thức mà còn hỗ trợ học tập và làm việc hiệu quả hơn.